Factorials
December 14, 2020
Mathematicians are
reserved people who generally stay in quiet
rooms for extended periods as they scratch out their latest
proof with
pencil on
paper.
Experimental mathematicians are somewhat more
agitated, since they are
stimulated by the glow of their
display screens and the
hum of their
computer fan. I've heard that the proof of
Fermat's last theorem was
celebrated by adding an extra
teaspoonful of
honey to their
teacups at
afternoon tea.[1]
That's why I was surprised as a
student to learn that the
symbol for the
factorial operation was an
exclamation point. The factorial N! of a
number, N, is the
product of all
positive integers less than or equal to N; that is, (N)(N-1)(N-2)...(1). As an example, 5! is (5)(4)(3)(2)(1) = 120, and 0! is arbitrarily defined as equal to 1.
Mathematics developed because of its utility in solving problems in ordinary life, such as
calculating land areas for
taxes. The
Greek philosopher,
Thales of Miletus (c. 624-c. 545 BC), used
geometry to determine the
distance to
ships from a
shoreline, which was the same method of
proportional triangles that I learned as a
Boy Scout for finding the
width of a
river.
Renaissance mathematicians took an interest in the calculation of
gambling odds, such as the
probability of
rolling certain number
sums with
dice, and that's when factorials became useful.

In the simple days of my childhood (BC, as in "before computers"), there weren't many things to occupy a child's time; so, my brothers and I would often play card games.
Shown here is a straight poker hand, Ace high. If the Queen of Hearts were instead a Queen of Spades, the hand would be a Royal Flush, the best hand in Poker. The probability of being dealt such a hand is just 0.000154% (see below). (Wikimedia Commons image by sunkiddance.)
There are two operations involving factorials that are used in determining probabilities; namely,
combinations and
permutations. When the
order of selecting objects doesn't matter, we use a combination, and when the order is important, we use a permutation. A combination of k objects taken from a collection of n objects, C(n,k), is given as (n!)/(k!(n-k)!), and the permutation of n things selected from k choices, P(n,k), is given as (n!)/((n-k)!). One interesting fact is that what's called a
combination lock is actually a permutation lock.
As an example of a combination, let's say you've just had a bad
week, and you were interested in how each week in your
year of 52 weeks relates to another. You would calculate the combination of 52 things taken two at a time, C(52,2) = (52!)/(2!(52-2)!) = 1,326. Likewise for
poker hands, the probability of drawing a particular five card
hand from the deck of 52 unique cards (thirteen different values in four
suits) would be C(52,5) = (52!)/(5!(52-5)!) = one chance out of 2,598,960, or 0.000038477%.
There are four different ways to get a
Royal Flush, since there are four suits, so this probability can be multiplied by four to give a 0.000154% chance of being
dealt a Royal Flush. As an example of permutations, perhaps you want to create a
composite month of four weeks from the 52 weeks of the year. There are P(52,4) = 52!/(52-4)! = 6,497,400 different ways you can do this.
The factorial of numbers blows up quite quickly, as the following table shows.
| N |
N! |
| 1 |
1 |
| 10 |
3.628800 x 106 |
| 100 |
9.332621544 x 10157 |
| 1000 |
4.023872601 x 102567 |
| 10000 |
2.846259681 x 1035659 |
| 100000 |
2.824229408 x 10456573 |
| 1000000 |
8.263931688 x 105565708 |
Excel and
Gnumeric can only calculate factorials up to 170! = 7.257416e+306. This is also the limit for
MATLAB, a
computation and
graphing application used by many
researchers. I don't use MATLAB, or the similar
Mathematica application, since I'm an advocate for
free and open source software (FOSS). I'm as impressed by the high
cost of these applications as I am by their functionality.
It's unfortunate that
software companies have embraced a
business model in which they
rent, rather than
sell, their software. The
economist,
Thorstein Veblen (a.k.a., Torsten Veblen), wrote about "charging what the market will bear" in his 1899 book,
The Theory of the Leisure Class.[2]

Thorstein (Torsten) Veblen (1857-1929).
Veblen's "The Theory of the Leisure Class" introduced the term, "conspicuous consumption."
Conspicuous consumption is the purchase of lavishly expensive, or ephemeral and impractical, goods and services simply as a way of displaying income or wealth.
(Wikimedia Commons image, modified for artistic effect)
Although I use the
PHP language for simple tasks, my usual computation language for mathematics is the
C programming language. C code, compiled using the
GCC compiler and a
long long int type for N will only give factorials up to 20! = 2432902008176640000 (2.4329 x 10
18). However, there is a
library that allows much larger factorials than this.
The
GNU Multiple Precision Arithmetic Library (GMP) is easily installed on a
Linux computer. This library extends our access to large numbers considerably, although there are limits imposed by
memory space on a
desktop computer. I haven't used GMP in more than a
decade, but I was able to hack together a program to calculate factorials, and also the
approximation equation for factorials developed by mathematician,
James Stirling (1692-1770) (Source code
here). Another approximation, as described below, gives much better values, and I coded this in the program, also.[3]
Of course, it's tedious to multiply many numbers together, especially when you don't need a
precise result. That's why Stirling's factorial approximation equation is useful. As sometimes happens in
science and mathematics, this equation was named after Stirling, although it was first stated by
Abraham de Moivre (1667-1754). De Moivre was interested in probabilities, and he was the
author of the first
textbook on probability,
The Doctrine of Chances (1718). Stirling's equation,
asymptotic to the actual value of n! (it's better as n gets larger), is as follows:
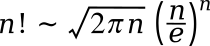
Centuries later,
preeminent number theorist,
Srinivasa Ramanujan (1887-1920), discovered a more precise approximation. This was written only in a
notebook, but it was eventually
published in 1988.[4]
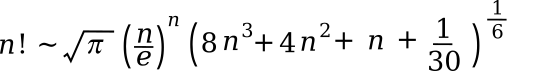
So, how much better is Ramanujan's approximation than Stirling's? One glance at the following
graph, derived from
data generated by my evaluation program, tells all. The percentage error of Ramanujan's approximation at n=500 is just 8.1958 x 10
-7
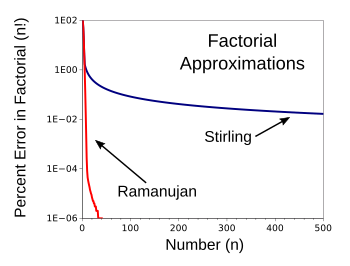
Stirling's Factorial Approximations, compared to the approximation created by Ramanujan, as calculated by my computer program.
Ramanujan's simple equation wins by a wide margin.
(Graphed using Gnumeric
![]()
References:
- This stereotyping is clearly exaggerated, but it makes for an interesting story.
- Thorstein Veblen, "The Theory of the Leisure Class," 1.4 MB PDF File, via Law in Contemporary Society Web Site, Columbia Law School.
- Sidney A. Morris, "Tweaking Ramanujan's Approximation of n!," arXiv, October 29, 2020.
- S. Ramanujan, The lost notebook and other unpublished papers, S.Raghavan and S. S. Rangachari, Eds., Springer, New York, 1988, ISBN: 978-3540187264 (Via Amazon).
Linked Keywords: Mathematician; reserved; room; mathematical proof; pencil; paper; experimental mathematics; experimental mathematician; agitated; stimulated; computer monitor; display screen; hum; computer fan; Fermat's last theorem; party; celebrate; teaspoon; teaspoonful; honey; teacups; afternoon tea; student; mathematical symbol; factorial; operation (mathematics); exclamation mark; exclamation point; natural number; product (mathematics); positive integer; calculation; calculating; land; area; tax; Ancient Greek philosophy; Greek philosopher; Thales of Miletus (c. 624-c. 545 BC); geometry; distance; ship; shoreline; proportionality (mathematics); proportional; triangle; Boy Scouts of America; width; river; Renaissance; fixed-odds betting; gambling odds; poker probability; dice roll; addition; sum; dice; childhood; computer; brother; card game; straight poker hand, Ace high; Queen (playing card); Queen of Hearts; Queen of Spades; Royal Flush; card game dealing; Wikimedia Commons; sunkiddance; combination; permutation; hierarchy; order; combination lock; week; year; poker probability; poker hand; playing card suit; straight flush; Royal Flush; composite; month; Excel; Gnumeric; MATLAB; computation; chart; graph; application software; research; researcher; Mathematica; free and open source software (FOSS); cost; software company; business model; rent; sell; economist; Thorstein Veblen; The Theory of the Leisure Class; Thorstein (Torsten) Veblen (1857-1929); conspicuous consumption; lavishly expensive; ephemeral; goods; service (economics); income; wealth; PHP language; C programming language; GNU Compiler; C data type; long long int type; library (computing); GNU Multiple Precision Arithmetic Library (GMP); Linux; computer memory; memory space; desktop computer; decade; Stirling's approximation equation for factorials; James Stirling (1692-1770); stirling ramanujan.c; accuracy and precision; precise; science; Abraham de Moivre (1667-1754); author; textbook; The Doctrine of Chances; asymptote; asymptotic; century; greatness; preeminent; number theory; number theorist; Srinivasa Ramanujan (1887-1920); notebook; academic publishing; published<; Cartesian coordinate system; data.