Tikalon Blog by Dev Gualtieri

Tikalon Header

Negative Thermal Expansion

November 11, 2011

The vast majority of materials expand when heated, an effect known as thermal expansion . Thermal expansion causes major problems in the manufacture of useful articles. Unless thermal expansion is taken into account during design , camera lenses will defocus , and parts carefully fit at room temperature will fracture as the temperature is increased.

The linear thermal expansion of materials is quantified by the thermal expansion coefficient , which generally goes by the symbol, alpha (α),

α = (1/L)(∂L/∂T)

for which L is the gauge length, T is the temperature , and the dimensions are usually (1/°C). The following table lists the thermal expansion coefficient at room temperature (20°C) for a variety of materials.

Material	α (10^-6/°C)	Material	α (10^-6/°C)
Ethanol	250	Carbon steel	10.8
Water	69	Glass	8.5
Mercury	61	Alumina	7.8
Aluminium	23	Tungsten	4.5
Stainless steel	17.3	Borosilicate glass	3.3
Copper	17	Invar	1.2
Nickel	13	Diamond	1
Concrete	12	Fused quartz	0.59

You can see from the table that hydrogen-bonded liquids (ethanol and water) have a large thermal expansion; and also why mercury was popular in the past for thermometers . It's intuitively easy to see why thermal expansion should exist. Temperature is simply the vibration of atoms, and the vibrational energy will act against the bonding forces that hold atoms together. An end consequence of this is the eventual vaporization of materials into a gas .

That's why negative thermal expansion (NTE) is so unusual. A few isolated examples of NTE were discovered over the years, one of which is water between freezing and 3.984°C.[1] There are so many unusual things about water, that even this brief excursion into NTE didn't raise too many eyebrows. Silicon exhibits NTE in a temperature range of 18 - 120 K .

Hope that some utility can be gained from NTE began in 2004 with the discovery of NTE in an oxide of zirconium and tungsten , cubic zirconium tungstate , ZrW₂O₈.[2-3] Unlike water, where the temperature range for NTE is very limited, or silicon, where the temperatures are too low to be really useful, zirconium tungstate exhibits NTE from almost absolute zero to 775 °C. Analogs of this material in which hafnium substitutes for zirconium, and molybdenum substitutes for tungsten, also exhibit NTE.

In 2010, scandium fluoride (ScF₃), a material with a different crystal structure , was discovered to have an NTE as large as -14 ppm/°C at temperatures from 60-110 K.[4] Its NTE increases to become equivalent to that of zirconium tungstate at room temperature, and the thermal expansion finally becomes positive above 1100 K.[4]

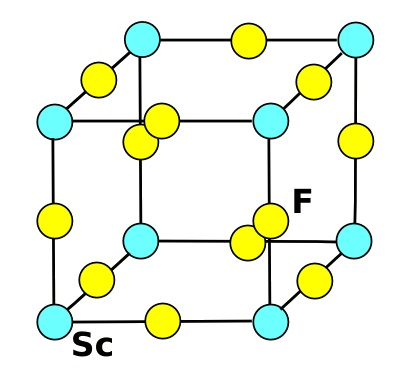The crystal structure of scandium fluoride

The crystal structure of scandium fluoride.

Drawing by author, rendered with Inkscape.

A research team from the Department of Applied Physics and Materials Science of the California Institute of Technology (Pasadena, California), and the Neutron Scattering Science Division of Oak Ridge National Laboratory (Oak Ridge, Tennessee), has just performed a study to elucidate the mechanism of scandium fluoride's NTE.[5-8] The study was somewhat enabled by the simple lattice structure of the scandium fluoride crystal, as shown in the above figure. The neutron scattering at the Oak Ridge National Laboratory Spallation Neutron Source allowed measurement of the atomic vibrations.[7]

The neutron scattering revealed that all of the atomic resonances remained roughly constant as the temperature was changed, except for one that shifted to higher frequency , an indication of increased bonding force.[6] What apparently happens is that the fluorine atoms are vibrating in a direction transverse to the linear chains of scandium-fluorine-scandium atoms. This is apparently the root cause of the negative thermal expansion.[7]

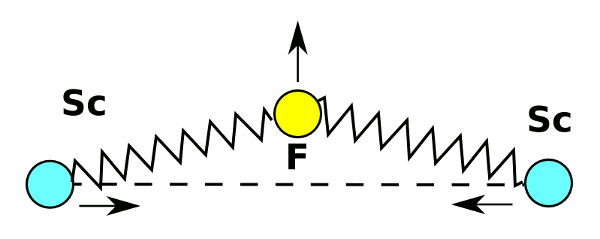Principle of negative thermal expansion in scandium fluoride

Principle of negative thermal expansion in scandium fluoride. The fluorine atoms vibrate in a transverse direction to the scandium atoms to pull them together. Drawing by author, rendered with Inkscape.

One curious finding is that the restoring force of the fluorine vibration is a function of the fourth power of the displacement . This quartic oscillation is unlike the quadratic (second power) oscillation that's found in atomic vibrations and harmonic oscillators .[7] Says Brent Fultz , study coauthor and Professor of Materials Science and Applied Physics at Caltech, "A nearly pure quantum quartic oscillator has never been seen in atom vibrations in crystals."[7]

The research team speculates that quartic oscillator materials may also be good thermal insulating materials. NTE materials can be combined with other materials to produce zero expansion materials, at least over a small temperature range. Such materials would be useful in optics, but also things as mundane as dental restoration .[6]

References: