Eratosthenes
March 17, 2011 When I was a child, my parents must have noticed my mathematical bent, since I received as a Christmas present one year "The Giant Golden Book of Mathematics."[1] This oversized book (10-1/2 inches wide by 12 inches tall) still sits on my bookshelf as an inspiration. It's also a reminder that dead-tree books are better than e-books in many cases. This book has one chapter, "Numbers We Cannot Split," about prime numbers and the Sieve of Eratosthenes. Eratosthenes (c. 276 BC - c. 195 BC) was a Greek mathematician and a friend of Archimedes. He's best know for the prime number sieve, which is understandable to most schoolboys. The sieve has been improved somewhat over the years, the improvements being in the means of quickly eliminating the non-primes (composite numbers) from the integers. Eratosthenes has us just cross out every number divisible by two, then three, five, etc., and this method will, of course, work. A program to do this is easy to write, and I have some source code here.
Eratosthenes at work. Engraving after a work by the French painter Gustave Courtois (1853-1923), via arXiv.[2]
An Indian schoolboy, S. P. Sundaram, perhaps inspired by the role model of Ramanujan, found a better technique in 1934.[3] To find all primes up to about 2n, Sundaram's sieve has us cast out all numbers (i + j + 2ij), where i and j are positive integers, (i + j + 2ij) is less than or equal to n, and i < j. The remaining numbers are then multiplied by two and added to one. This gives you all prime numbers (except for 2) below 2n + 2. A Canadian high school student, Bai Li, writes a very nice blog, and he has posted some code that uses Sundaram's technique.[4]
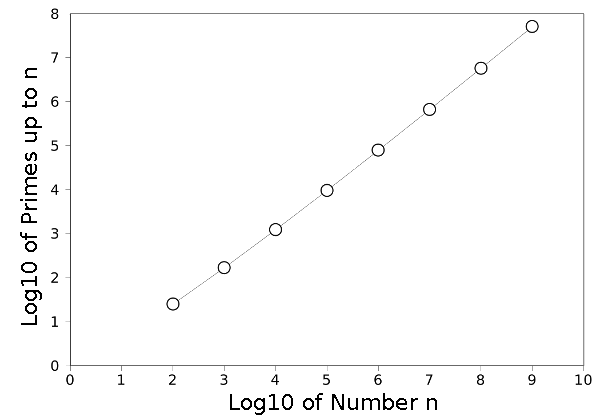Number of primes less than n. A log10-log10 scale is used with data from my primes program. Many more values can be found here. Graph rendered using Gnumeric.
The idea that, on a lark, I can write a program to find the first 100 million prime numbers, shows how far we've come from the "Golden Book" days. The figure above shows one of the regularities of prime numbers that makes them interesting. However, prime number theory has advanced well beyond mere lists of primes, and it's too big a topic for a blog article; so I'll mention another discovery of Eratosthenes. He measured the size of the Earth quite accurately more than two millennia ago.
Pliny the Elder, whom I've mentioned quite a few times in previous articles, reported on Eratosthenes'' measurement.[5]
And thus much of the length and breadth of the earth, which I thought worth the writing. Now the universall compasse and circuit thereof, Eratosthenes (a great Clerke verily for all kind of literature, and in this knowledge above all others doubtlesse most cunning, and whome I see of all men approved and allowed) hath set downe to be 252000 stadia. Which measure, by the Romanes account and reckoning, amounteth to 300 hundred and 15 hundred miles. A wonderous bold attempt of his! but yet so exquisitely calculated and contrived by him, that a shame it were not to beleeve him.Pliny had a way with words, but not much for mathematical exposition. Khristo N. Boyadzhiev, in an article posted to arXiv last year,[2] interprets the text as saying that Earth's circumference is 39,375 km, which is extremely close to the actual equatorial value of 40,075 km. Pliny didn't quite believe that such a value could be calculated. Boyadzhiev writes that Pliny thought you would need to travel to Earth's center to judge its radius, and this practical outlook was the reason why there was no tradition of science in Ancient Rome.
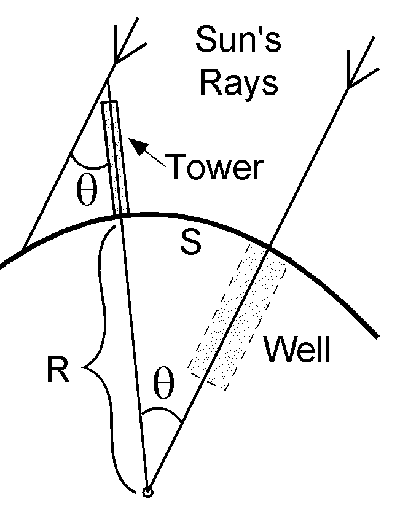 | Eratosthenes' measurement of Earth's radius. The angle θ is 7.2 degrees, and the circle arc S is 787.5 km. |
R = S/θ,where θ is in radians. For 7.2 degrees, this is 0.1256637 radians, giving a radius (R) of 6,266.7259 km and a circumference of 39,374 km. There are some "urban legends" about Christopher Columbus, one of which is that he made his historic voyage to prove the world was round. It's fairly certain that Columbus knew about Earth's spherical shape, but he didn't have a good idea of its size. His intent was to sail to India by going west, instead of east; instead, he bumped into the Americas and called the inhabitants "Indians." Perhaps if he had read Eratosthenes, he would have known better. Then again, if he had known better, he might not have made his trip.
References:
- Irving Adler, "The Giant Golden Book of Mathematics," Illustrated by Lowell Hess, Golden Press (New York, 1960), 92 pages.
- Khristo N. Boyadzhiev, "Eratosthenes and Pliny, Greek geometry and Roman follies," arXiv Preprint, June 15, 2010.
- Sieve of Sundaram page on Wikipedia.
- Sieve of Sundaram article on Bai Li's blog.
- Philemon Holland, translator (1601): G. Plinius Secundus The Historie of the World, Book II, Paragraph 247.
De longitudine ac latitudine haec sunt, quae digna memoratu putem. universum autem circuitum Eratosthenes, in omnium quidem litterarum subtilitate, set in hac utique praeter ceteros solers, quem cunctis probari video, CCLII milium stadiorum prodidit, quae mensura Romana conputatione efficit trecentiens quindeciens centena milia passuum: inprobum ausum, verum ita subtili argumentatione conprehensum, ut pudeat non credere.
- Chris Caldwell, "Online prime test," Prime Curios! web site at The University of Tennessee at Martin.
- Sieve of Sundaram page on Wikipedia.